Replica Method for the Sherrington-Kirkpatrick Model

This note reviews the replica symmetric solution of the SK model, including sufficiently detailed derivations, and then shows the phase diagrams of the order parameters and free energy by numerical calculations. The author acknowledges H. Nishimori’s book ¹ for its introduction to the mean-field theory of spin glass, and Haozhe Shan’s notes ², which contain extensive derivations and greatly assisted the author in following the derivation.

1. Introduction

The Hamiltonian of the Sherrington-Kirkpatrick model reads

where are Ising spins, the interaction between any two spins is a quenched variable with the Gaussian distribution .

The mean and variance are both proportional to to ensure the Hamiltonian is extensive. The probability of each configuration is given by the Gibbs-Boltzmann distribution , where is the partition function. We denote , so that the partition function is expressed as . The free energy can be calculated by the partition function as .

However, it is only the free energy for a fixed interaction sampled from the distribution. One not depended on any specific system sample can be obtain by the average over the distribution of , which is called the quenched average, or disorder average, or configurational average, and denoted by in this paper:

The dependence of on is so complex that it cannot be solved directly, and this is where the replica method comes into play.

2. Replica Method

The replica trick is a mathematical technique based on the application of the formula

In this case, the replica average of the partition function can be written as

where the explicit expression of the integral measure is given by the distribution of

Firstly, Eq. (4) can be calculated as

where the integral term in Eq. (6) is calculated as

and the following trick is used in Eq. (8)

Considering , i.e.

we have

and

Thus Eq. (10) is written as

where the following approximation in the large limit is used

In order to linearize the quadratic term on the exponential, it is useful to introduce the Hubbard-Stratonovich transform, an inverse application of the Gaussian integral, as follow

Let , and , then we have

Let , and , then we have

Then Eq. (19) can be written as

where we define

in Eq. (25) and used

In large limit, the integral in Eq. (26) can be calculated with the Laplace approximation, also known as the saddle-point approximation, i.e.

Let

and the result of the integral is

where we used Taylor expansion in Eq. (33), and . Through , we arrive at

The free energy density is finally written as

3. Replica Symmetry Ansatz

To continue solving Eq. (36), we need to consider the dependencies of and for different replica index. A naive idea is that they are independent of index, i.e. , , , also called replica symmetry ansatz. The replica symmetric free energy is written as

where .

The final item is calculated as

where we used Hubbard-Stratonovich transform again in Eq. (40) and reparameterized by a standard Gaussian variable , rewriting integral variables as Gaussian integral measures

The last item in Eq. (41) is calculated as

where we defined .

Finally, the replica symmetric free energy is

Through

we obtain a set of closed equations, called saddle point equations

4. Numerical Results

Considering a simple case where , we use numerical methods to iterate Eq. (56) and Eq. (57) to obtain the fixed points of order parameters and , and plot the phase diagrams as follows:

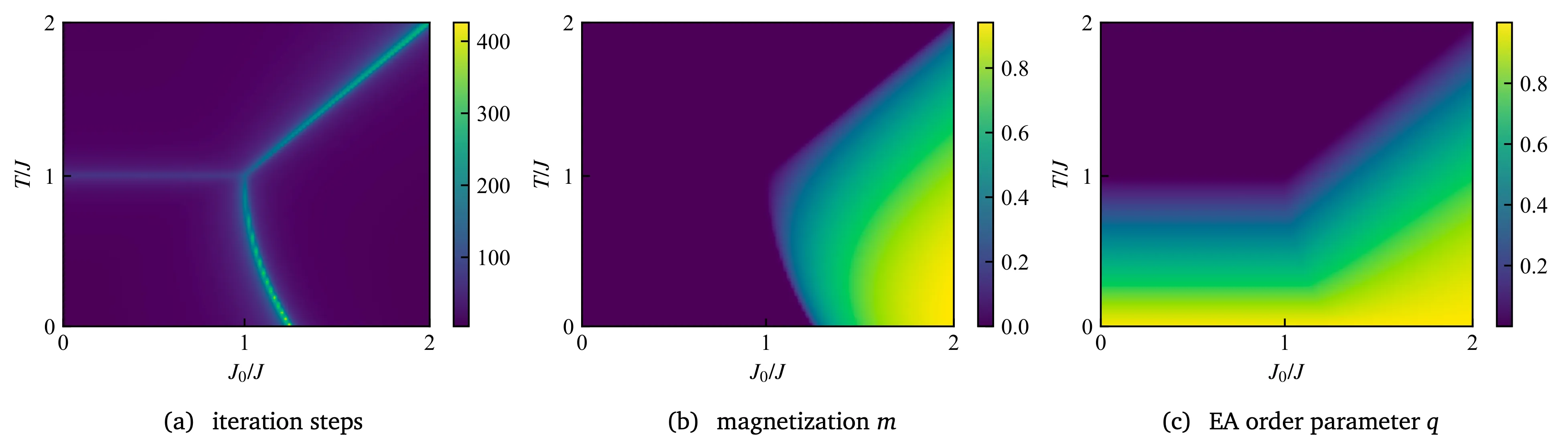
This results (especially the interaction steps) recover the well-known phase diagram of the SK model with three phases: ferromagnetic phase, paramagnetic phase, and spin glass phase.

Due to the Frustration, the spin in the SK model is frozen at low temperature, yet remains highly disordered, with the order parameter . But this is a phase different from the paramagnetic phase (also ) and is called the spin glass phase. In short, identifies the ferromagnetic phase, and the EA order parameter is introduced to distinguish between the paramagnetic phase () and the spin glass phase ().

Footnotes

1. H. Nishimori, Statistical Physics of Spin Glasses and Information Processing: An Introduction (Oxford, 2001) ↩

2. Replica calculations for the SK model, URL: hzshan.github.io/replica_method_in_SK_model.pdf ↩